Engineering Software
Otto Cycle Analysis -- Free One (1) Credit Hour of CE
Otto Cycle
Introduction
This section provides an Otto Cycle analysis when the working fluid is air.
Analysis
In the presented Otto Cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
Air enters a cylinder at point 1 when compression starts and it ends at point 2. Isentropic compression is considered with no entropy change. Heat addition starts at point 2 and it ends at point 3. At a constant volume, air gets heated and the working fluid temperature raises. Expansion starts at point 3 and it ends at point 4. Isentropic expansion is considered with no entropy change. Air heat rejection starts at point 4 and it ends at point 1. At a constant volume, air gets cooled and the working fluid temperature decreases. It should be mentioned that air at point 1 enters the compression process again and the cycle is repeated.
Figure 1 contains an Otto Cycle pressure vs volume diagram.
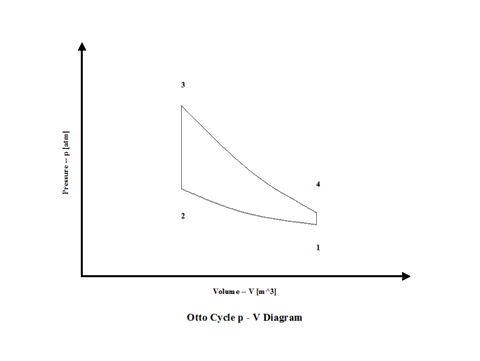
Figure 1 - Otto Cycle Pressure vs Volume Diagram
Figure 2 presents an Otto Cycle temperature vs entropy diagram.
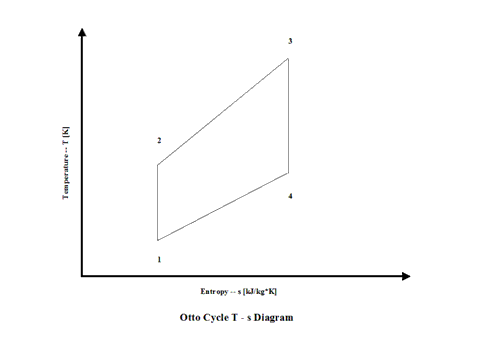
Figure 2 - Otto Cycle Temperature vs Entropy Diagram
Figure 3 presents the Otto Cycle efficiency as a function of the compression ratio. It should be noted that the inlet conditions are standard ambient conditions: temperature of 298 [K] and absolute pressure of 1 [atm].
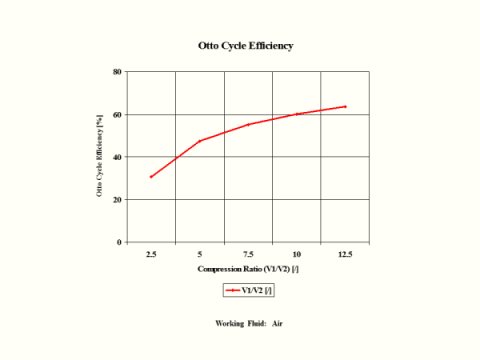
Figure 3 - Otto Cycle Efficiency
Figure 4 presents the Otto Cycle power output as a function of the combustion temperature and compression ratio. It should be noted that the number of revolutions is 60 [1/s] for given geometry of the four cylinder and four stroke Otto engine.
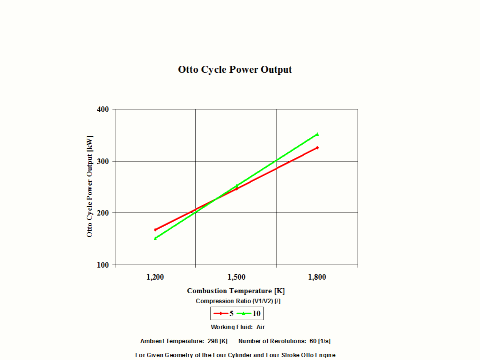
Figure 4 - Otto Cycle Power Output
One can notice that the Otto Cycle efficiency increases with an increase in the compression ratio values. One can notice that the Otto Cycle power output increases with an increase in the combustion temperature. The Otto Cycle power output is greater for the higher compression ratio values.
Assumptions
Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
Governing Equations
T2/T1 = (V1/V2)^(ϰ-1)
V1/V2 = (T2/T1)^1/(ϰ-1)
T3/T4 = (V4/V3)^(ϰ-1)
V4/V3 = (T3/T4)^1/(ϰ-1)
ϰ = cp/cv
cp - cv = R
pv = RT
w = qh - ql
qh = cv(T3 - T2)
ql = cv(T4 - T1)
w = cv(T3 - T2) - cv(T4 - T1)
W = (cv(T3 - T2) - cv(T4 - T1))m
efficiency = 1 - 1/compression ratio^(ϰ-1)
compression ratio = V1/V2
Input Data
T1 = 298 [K]
p1 = 1 [atm]
T3 = 1,200, 1,500 and 1,800 [K]
compression ratio = 2.5, 5, 7.5, 10 and 12.5 [/]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
Results
Otto Cycle Efficiency vs Compression Ratio
Compression
Ratio
[/]
2.5
5
7.5
10
12.5
Otto Cycle
Efficiency
[%]
30.7
47.5
55.3
60.2
63.6
Otto Cycle Power Output
Power Output
[kW]
Compression Ratio
[/]
5
15
Combustion
Temperature
[K]
1,200
167.1
151.2
1,500
246.4
251.7
1,800
325.6
352.2
Conclusions
The Otto Cycle efficiency increases with an increase in the compression ratio values. Also, the Otto Cycle power output increases with an increase in the combustion temperature. The Otto Cycle power output is greater for the higher compression ratio values.
References
JANAF Thermochemical Data - Tables, 1970