Engineering Software
Compression Analysis
Compression
Introduction
This section provides an isentropic compression analysis when the working fluid is air.
Analysis
In the presented compression analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
Air enters a compressor at point 1 and it exits the compressor at point 2. Isentropic compression is considered with no entropy change.
Figure 1 presents a compression schematic layout.
Figure 1 - Compression Schematic Layout
Figure 2 presents a compression temperature vs entropy diagram.
Figure 2 - Compression Temperature vs Entropy Diagram
Figure 3 presents compression specific power input requirements for a few typical compression ratio values. It should be noted that the air enters the compressor at standard ambient conditions of 298 [K] and 1 [atm] of absolute pressure.
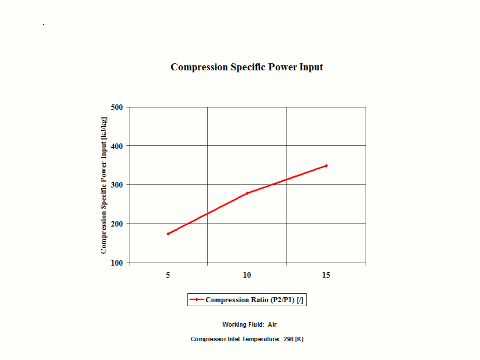
Figure 3 - Compression Specific Power Input
Figure 4 presents compression power input requirements for two typical compression ratio values and a few different working fluid mass flow rate values for a fixed compression inlet temperature.
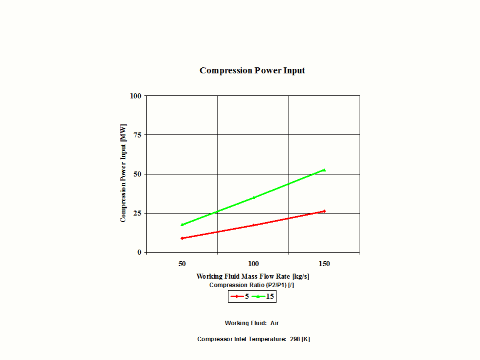
Figure 4 - Compression Power Input
One can notice that both compression specific power input and power input increase with an increase in the compression ratio values. As the working fluid mass flow rate increases for a fixed compression inlet temperature, the compression power input requirements increase too.
Assumptions
Working fluid is air. There is no friction and heat transfer. Compression is isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
Governing Equations
T2/T1 = (p2/p1)^(ϰ-1)/ϰ
ϰ = cp/cv
cp - cv = R
pv = RT
w = cp(T2 - T1)
W = cp(T2 - T1)m
Input Data
T1 = 298 [K]
p1 = 1 [atm]
p2 = 5, 10 and 15 [atm]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
m = 50, 100 and 150 [kg/s]
Results
Specific Power Input vs Compression Ratio
Compression Inlet Temperature = 298 [K]
Compression
Ratio
[/]
5
10
15
Specific Power
Input
[kW/kg/s]
174
278
349
Power Input vs Compression Ratio for a few Mass Flow Rates
Compression Inlet Temperature = 298 [K]
Power Input
[MW]
Compression Ratio
[/]
5
15
Mass Flow Rate
[kg/s]
50
8.7
17.5
100
17.4
34.9
150
26.0
52.4
Conclusions
Both compression specific power input and power input increase with an increase in the compression ratio values. As the working fluid mass flow rate increases for a fixed compression inlet temperature, the compression power input requirements increase too.
References
JANAF Thermochemical Data - Tables, 1970