Engineering Software
Power Cycles Analysis
This section provides free Power Cycles Analysis.
Power Cycles Analysis covers the following areas:
Carnot Cycle
Brayton Cycle -- Power Application
Brayton Cycle -- Propulsion Application
Otto Cycle
Diesel Cycle
Carnot Cycle
Introduction
This section provides a Carnot Cycle analysis when the working fluid is air.
Analysis
In the presented Carnot Cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
Air enters a compressor at point 1 and it exits the compressor at point 2. Isentropic compression is considered with no entropy change. Air enters a heat exchanger -- heat addition -- at point 2 and it exits the heat exchanger at point 3. At a constant temperature, heat addition takes place. Air enters a turbine at point 3 and it exits the turbine at point 4. Isentropic expansion is considered with no entropy change. Air enters a heat exchanger -- heat rejection -- at point 4 and it exits the heat exchanger at point 1. At a constant temperature, heat rejection takes place. It should be mentioned that air at point 1 enters the compressor and the cycle is repeated.
Figure 1 contains a Carnot Cycle schematic layout.
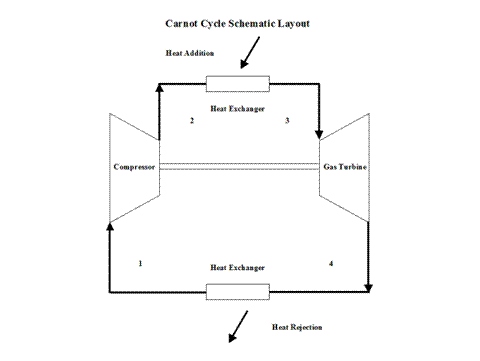
Figure 1 - Carnot Cycle Schematic Layout
Figure 2 presents a Carnot Cycle entropy vs temperature diagram.
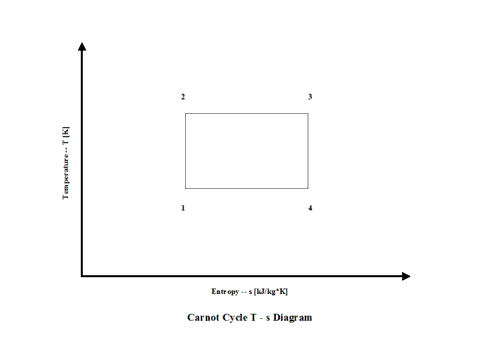
Figure 2 - Carnot Cycle Temperature vs Entropy Diagram
Figure 3 presents the Carnot Cycle efficiency as a function of the heat addition temperature. It should be noted that the inlet conditions are standard ambient conditions: temperature of 298 [K] and absolute pressure of 1 [atm].
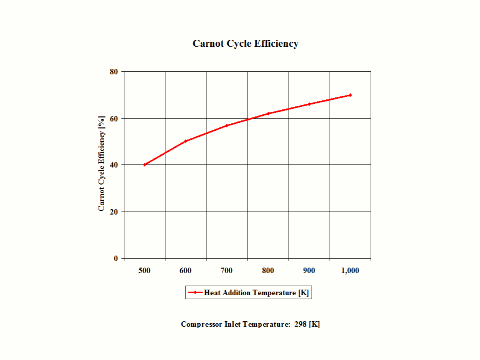
Figure 3 - Carnot Cycle Efficiency vs Heat Addition Temperature
Figure 4 presents the Carnot Cycle efficiency as a function of the heat rejection temperature. It should be noted that the turbine inlet temperature is at 800 [K].
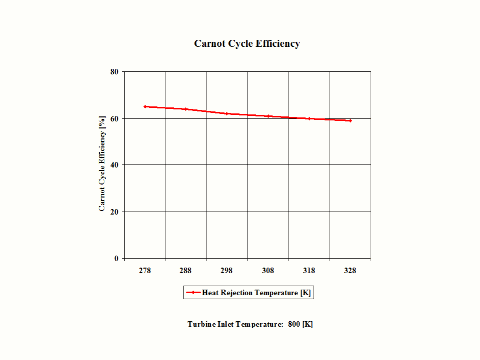
Figure 4 - Carnot Cycle Efficiency vs Heat Rejection Temperature
One can notice that the Carnot Cycle efficiency increases with an increase in the heat addition temperature when the heat rejection temperature does not change at all. One can notice that the Carnot Cycle efficiency decreases with an increase in the heat rejection temperature when the heat addition temperature does not change at all.
Assumptions
Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. During heat addition and heat rejection, the air temperature does not change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
Governing Equations
T2/T1 = (p2/p1)^(ϰ-1)/ϰ
T3/T4 = (p3/p4)^(ϰ-1)/ϰ
ϰ = cp/cv
cp - cv = R
pv = RT
efficiency = 1 - T1/T2
efficiency = 1 - TR/TA
Input Data
T1 = 298 [K]
p1 = 1 [atm]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
Results
Carnot Cycle Efficiency vs Heat Addition Temperature
Heat Rejection Temperature = 298 [K]
Heat Addition
Temperature
[K]
500
600
700
800
900
1,000
Carnot Cycle
Efficiency
[%]
40
50
57
62
66
70
Carnot Cycle Efficiency vs Heat Rejection Temperature
Heat Addition Temperature = 800 [K]
Heat Rejection
Temperature
[K]
278
288
298
308
318
328
Carnot Cycle
Efficiency
[%]
65
64
62
61
60
59
Conclusions
The Carnot Cycle efficiency increases with an increase in the heat addition temperature when the heat rejection temperature does not change at all. Furthermore, the Carnot Cycle efficiency decreases with an increase in the heat rejection temperature when the heat addition temperature does not change at all. The Carnot Cycle efficiency is not dependent on the working fluid properties.
References
JANAF Thermochemical Data - Tables, 1970
Brayton Cycle -- Power Application
Introduction
This section provides a Brayton Cycle analysis when the working fluid is air.
Analysis
In the presented Brayton Cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
A gas turbine is a heat engine that uses a high temperature, high pressure gas as the working fluid. Combustion of a fuel in air is usually used to produce the needed temperatures and pressures in the gas turbine, which is why gas turbines are often referred to as combustion turbines. Expansion of the high temperature, high pressure working fluid takes place in the gas turbine. The gas turbine shaft rotation drives an electric generator and a compressor for the working fluid, air, used in the gas turbine combustor. Many gas turbines also use a heat exchanger called a recouperator to impart turbine exhaust heat into the combustor's air/fuel mixture. Gas turbines produce high quality heat that can be used to generate steam for combined heat and power and combined-cycle applications, significantly enhancing efficiency.
The initial state of the working fluid, air, is assumed to be at point 1 at the atmospheric conditions, 298 [K] temperature and 1 [atm] pressure. Air is compressed, isentropically, along line 1-2 by a compressor and enters a combustor. At a constant pressure, combustion takes place (fuel is added to the combustor and the air temperature raises) and/or heat gets added to air. High temperature air exits the combustor at point 3. Then air enters a gas turbine where an isentropic expansion occurs, producing power. Air exits the gas turbine at point 4. It should be mentioned that air at point 1 enters the compressor and the cycle is repeated.
A schematic layout of the ideal, open Brayton Cycle is shown in Figure 1.
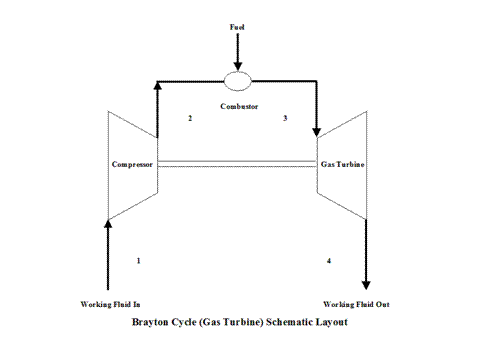
Figure 1 - Brayton Cycle Schematic Layout
Figure 2 presents a Brayton Cycle temperature vs entropy diagram.
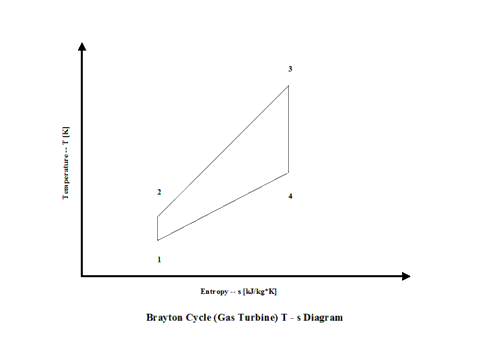
Figure 2 - Brayton Cycle Temperature vs Entropy Diagram
It should be pointed out that this material deals with the open Brayton Cycle. The way how the T - s diagram is presented, it describes a closed Brayton Cycle -- this would require a heat exchanger after point 4 where the working fluid would be cooled down to point 1 and the cycle repeats. Therefore, the T - s diagram is presented as a closed Brayton Cycle to allow easier understanding and derivation of the Brayton Cycle thermal efficiency -- heat addition and heat rejection.
The gas turbine and compressor are connected by shaft so the considerable amount of work done on the gas turbine is used to power the compressor.
It can be noticed from the T - s diagram that the work done on the gas turbine is greater than the work necessary to power the compressor -- constant pressure lines in the T - s diagram diverge by going to the right side (entropy wise).
Figure 3 presents the Brayton Cycle efficiency as a function of the compression ratio. It should be noted that the inlet conditions are standard ambient conditions: temperature of 298 [K] and absolute pressure of 1 [atm]. me. It's easy.
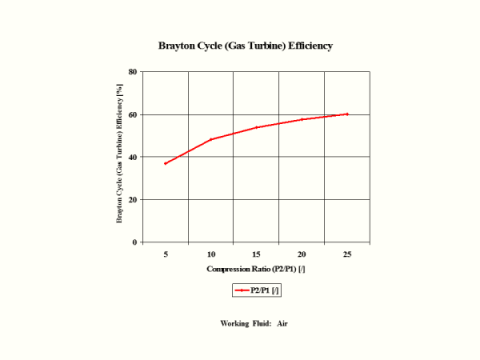
Figure 3 - Brayton Cycle Efficiency
Here, two general performance trends are considered. First, impact of the gas turbine inlet temperature and compression ratio values on the Brayton Cycle specific power output and second, impact of the working mass flow rate for a fixed gas turbine inlet temperature on the Brayton Cycle power output.
Figure 4 presents the results of the first performance trend, while Figure 5 presents the results of the second trend.
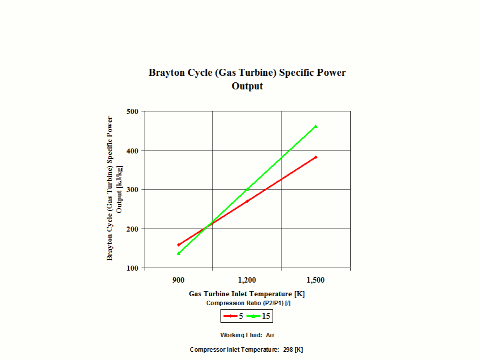
Figure 4 - Brayton Cycle Specific Power Output
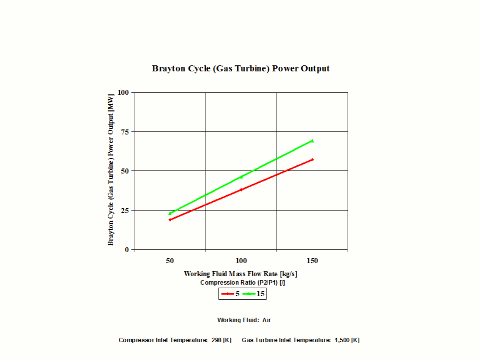
Figure 5 - Brayton Cycle Power Output
One can notice that the Brayton Cycle efficiency increases with an increase in the compression ratio values. One can notice that the Brayton Cycle specific power output increases with an increase in the gas turbine inlet temperature. Furthermore, the increase is greater for the higher compression ratio values.
One can notice that the Brayton Cycle power output increases with an increase in the working fluid mass flow rate for a fixed gas turbine inlet temperature. The increase is greater for the higher compression ratio values.
Assumptions
Working fluid is air. There is no friction. Compression and expansion processes are reversible and adiabatic -- isentropic. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas --specific heat has a constant value.
Governing Equations
T2/T1 = (p2/p1)^(ϰ-1)/ϰ
p2/p1 = (T2/T1)^ϰ/(ϰ-1)
T3/T4 = (p3/p4)^(ϰ-1)/ϰ
p3/p4 = (T3/T4)^ϰ/(ϰ-1)
ϰ = cp/cv
cp - cv = R
pv = RT
w = qh - ql
qh = cp(T3 - T2)
ql = cp(T4 - T1)
w = cp(T3 - T2) - cp(T4 - T1)
W = (cp(T3 - T2) - cp(T4 - T1))m
efficiency = 1 - 1/rp^(ϰ-1)/ϰ
rp = p2/p1
Input Data
T1 = 298 [K]
p1 = 1 [atm]
T3 = 900, 1,200 and 1,500 [K]
p3 = 5, 10, 15, 20 and 25 [atm]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
m = 50, 100 and 150 [kg/s]
Results
Brayton Cycle Efficiency vs Compression Ratio
Compression
Ratio
[/]
5
10
15
20
25
Brayton Cycle
Efficiency
[%]
36.92
48.22
53.87
57.53
60.16
Compression
Ratio
[/]
5
10
15
20
25
Brayton Cycle
Efficiency
[%]
36.92
48.22
53.87
57.53
60.16
Specific Power Output vs Compression Ratio
for a few Gas Turbine Inlet Temperature Values
Specific Power Output
[kW/kg/s]
Compression Ratio
[/]
5
15
Gas Turbine Inlet
Temperature
[K]
900
159
137
1,200
270
300
1,500
381
462
Power Output vs Compression Ratio
for a few Mass Flow Rates
Gas Turbine Inlet Temperature = 1,500 [K]
Power Output
[MW]
Compression Ratio
[/]
5
15
Mass Flow Rate
[kg/s]
50
19.1
23.1
100
38.1
46.2
150
57.2
69.3
Conclusions
The Brayton Cycle efficiency depends on the compression ratio and working fluid properties. The efficiency increases with an increase in the compression ratio values. Also, the efficiency increases with the higher value for kappa, ϰ, which is a ratio of gas specific heat values (cp/cv).
The Brayton Cycle specific power output increases with an increase in the gas turbine inlet temperature. Furthermore, the increase is greater for the higher compression ratio values. The Brayton Cycle power output increases with an increase in the working fluid mass flow rate for a fixed gas turbine inlet temperature. The increase is greater for the higher compression ratio values.
References
JANAF Thermochemical Data - Tables, 1970
I'm a paragraph. Click here to add your own text and edit me. It's easy.
Brayton Cycle -- Propulsion Application
Introduction
This section provides a Brayton Cycle analysis when the working fluid is air.
Analysis
In the presented Brayton Cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
A gas turbine is a heat engine that uses a high temperature, high pressure gas as the working fluid. Combustion of a fuel in air is usually used to produce the needed temperatures and pressures in the gas turbine, which is why gas turbines are often referred to as combustion turbines. Expansion of the high temperature, high pressure working fluid takes place in the gas turbine. The gas turbine shaft rotation drives an electric generator and a compressor for the working fluid, air, used in the gas turbine combustor. Many gas turbines also use a heat exchanger called a recouperator to impart turbine exhaust heat into the combustor's air/fuel mixture. Gas turbines produce high quality heat that can be used to generate steam for combined heat and power and combined-cycle applications, significantly enhancing efficiency.
The initial state of the working fluid, air, is assumed to be at point 1 at the atmospheric conditions, 298 [K] temperature and 1 [atm] pressure. Air is compressed, isentropically, along line 1-2 by a compressor and enters a combustor. At a constant pressure, combustion takes place (fuel is added to the combustor and the air temperature raises) and/or heat gets added to air. High temperature air exits the combustor at point 3. Then air enters a gas turbine where an isentropic expansion occurs, producing power. Air exits the gas turbine at point 4. It should be mentioned that air at point 1 enters the compressor and the cycle is repeated.
Figure 1 presents a Brayton Cycle schematic layout.
Figure 1 - Brayton Cycle Schematic Layout
Figure 2 presents a Brayton Cycle temperature vs entropy diagram
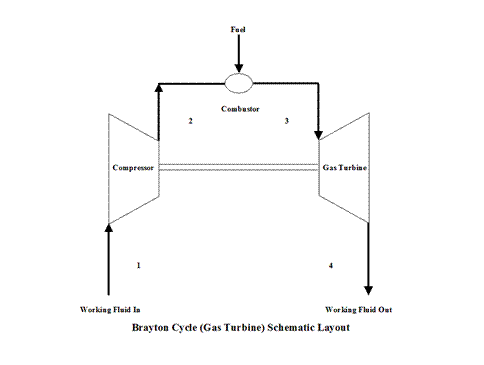
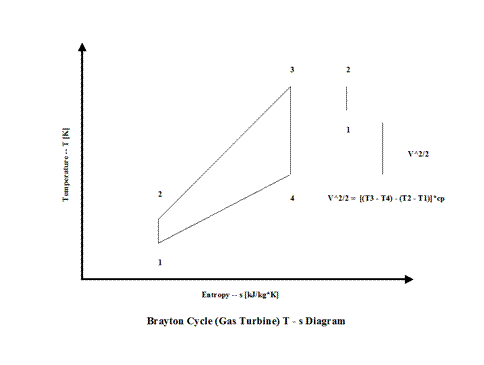
Figure 2 - Brayton Cycle Temperature vs Entropy Diagram
In order to keep the scope of thrust analysis simple, air exiting turbine expands to the atmospheric conditions -- exit pressure is equal to the ambient pressure (p1= p4 ).
It should be pointed out that this material deals with the open Brayton Cycle. The way how the T - s diagram is presented, it describes a closed Brayton Cycle -- this would require a heat exchanger after point 4 where the working fluid would be cooled down to point 1 and the cycle repeats. Therefore, the T - s diagram is presented as a closed Brayton Cycle to allow easier understanding and derivation of the Brayton Cycle thermal efficiency -- heat addition and heat rejection.
The gas turbine and compressor are connected by shaft so the considerable amount of work done on the gas turbine is used to power the compressor.
Propulsion is provided by the difference of gas turbine expansion minus the compressor power requirements.
It can be noticed from the T - s diagram that the work done on the gas turbine is greater than the work necessary to power the compressor -- constant pressure lines in the T - s diagram diverge by going to the right side (entropy wise).
Figure 3 presents the Brayton Cycle efficiency as a function of the compression ratio. It should be noted that the inlet conditions are standard ambient conditions: temperature of 298 [K] and absolute pressure of 1 [atm].
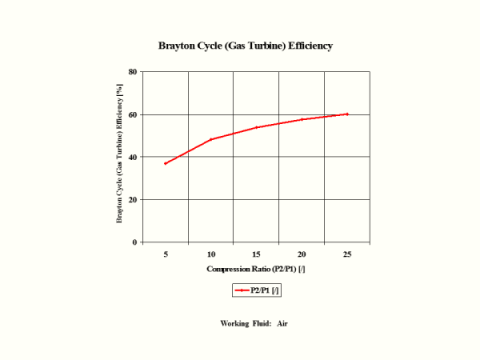
Figure 3 - Brayton Cycle Efficiency
Here, two general performance trends are considered. First, impact of the gas turbine inlet temperature and compression ratio on the Brayton Cycle specific propulsion output and second, impact of the working mass flow rate for a fixed gas turbine inlet temperature on the Brayton Cycle propulsion output.
Figure 4 presents the results of the first performance trend, while Figure 5 presents the results of the second trend.
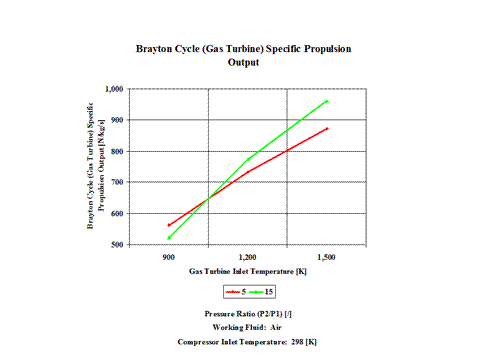
Figure 4 - Brayton Cycle Specific Propulsion Output
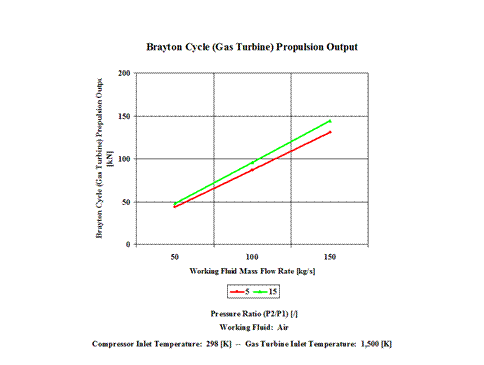
Figure 5 - Brayton Cycle Propulsion Output
One can notice that the Brayton Cycle efficiency increases with an increase in the compression ratio values. One can notice that the Brayton Cycle specific power output increases with an increase in the gas turbine inlet temperature. Furthermore, the increase is greater for the higher compression ratio values.
One can notice that the Brayton Cycle propulsion output increases with an increase in the working fluid mass flow rate for a fixed gas turbine inlet temperature. The increase is greater for the higher compression ratio values.
Assumptions
Working fluid is air. There is no fricion. Compression and expansion processes are reversible and adiabatic -- isentropic. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas --specific heat has a constant value.
Governing Equations
T2/T1 = (p2/p1)^(ϰ-1)/ϰ
p2/p1 = (T2/T1)^ϰ/(ϰ-1)
T3/T4 = (p3/p4)^(ϰ-1)/ϰ
p3/p4 = (T3/T4)^ϰ/(ϰ-1)
ϰ = cp/cv
cp - cv = R
pv = RT
w = qh - ql
qh = cp(T3 - T2)
ql = cp(T4 - T1)
w = cp(T3 - T2) - cp(T4 - T1)
W = (cp(T3 - T2) - cp(T4 - T1))m
efficiency = 1 - 1/rp^(ϰ-1)/ϰ
rp = p2/p1
v^2/2 = cp((T3 - T2) - (T4 - T1))
v = (2cp((T3 - T2) - (T4 - T1)))^1/2
Thrust = vm
Input Data
T1 = 298 [K]
p1 = 1 [atm]
T3 = 900, 1,200 and 1,500 [K]
p3 = 5, 10, 15, 20 and 25 [atm]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
m = 50, 100 and 150 [kg/s]
Results
Brayton Cycle Efficiency vs Compression Ratio
Compression
Ratio
[/]
5
10
15
20
25
Brayton Cycle
Efficiency
[%]
36.92
48.22
53.87
57.53
60.16
Compression
Ratio
[/]
5
10
15
20
25
Brayton Cycle
Efficiency
[%]
36.92
48.22
53.87
57.53
60.16
Specific Propulsion Output vs Compression Ratio
for a few Gas Turbine Inlet Temperature Values
Specific
Propulsion
[N/kg/s]
Compression Ratio
[/]
5
15
Gas Turbine Inlet
Temperature
[K]
900
563
524
1,200
734
774
1,500
872
961
Propulsion Output vs Compression Ratio
for a few Mass Flow Rates
Gas Turbine Inlet Temperature = 1,500 [K]
Propulsion Output
[kN]
Compression Ratio
[/]
5
15
Mass Flow Rate
[kg/s]
50
43.61
48.06
100
87.23
96.11
150
130.85
144.17
Conclusions
The Brayton Cycle efficiency depends on the compression ratio and working fluid properties. The efficiency increases with an increase in the compression ratio values. Also, the efficiency increases with the higher value for ϰ, which is a ratio of gas specific heat values (cp/cv).
The Brayton Cycle specific propulsion increases with an increase in the gas turbine inlet temperature. Furthermore, the increase is greater for the higher compression ratio values. The Brayton Cycle propulsion increases with an increase in the working fluid mass flow rate for a fixed gas turbine inlet temperature. The increase is greater for the higher compression ratio values.
References
JANAF Thermochemical Data - Tables, 1970
Otto Cycle
Introduction
This section provides an Otto Cycle analysis when the working fluid is air.
Analysis
In the presented Otto Cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
Air enters a cylinder at point 1 when compression starts and it ends at point 2. Isentropic compression is considered with no entropy change. Heat addition starts at point 2 and it ends at point 3. At a constant volume, air gets heated and the working fluid temperature raises. Expansion starts at point 3 and it ends at point 4. Isentropic expansion is considered with no entropy change. Air heat rejection starts at point 4 and it ends at point 1. At a constant volume, air gets cooled and the working fluid temperature decreases. It should be mentioned that air at point 1 enters the compression process again and the cycle is repeated.
Figure 1 contains an Otto Cycle pressure vs volume diagram.
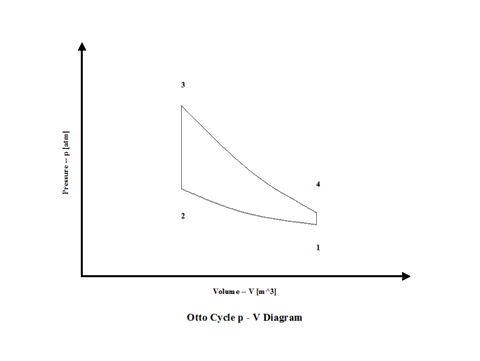
Figure 1 - Otto Cycle Pressure vs Volume Diagram
Figure 2 presents an Otto Cycle temperature vs entropy diagram.
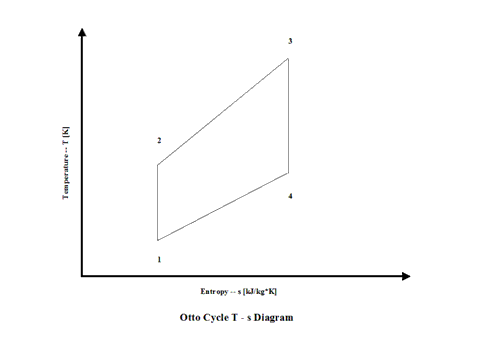
Figure 2 - Otto Cycle Temperature vs Entropy Diagram
Figure 3 presents the Otto Cycle efficiency as a function of the compression ratio. It should be noted that the inlet conditions are standard ambient conditions: temperature of 298 [K] and absolute pressure of 1 [atm].
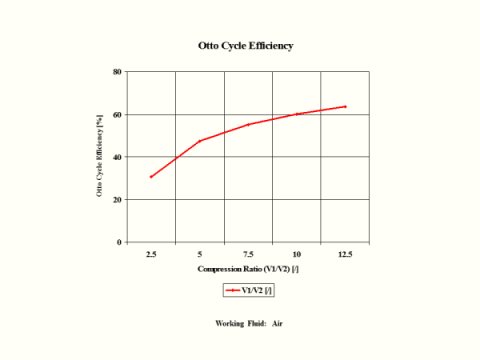
Figure 3 - Otto Cycle Efficiency
Figure 4 presents the Otto Cycle power output as a function of the combustion temperature and compression ratio. It should be noted that the number of revolutions is 60 [1/s] for given geometry of the four cylinder and four stroke Otto engine.
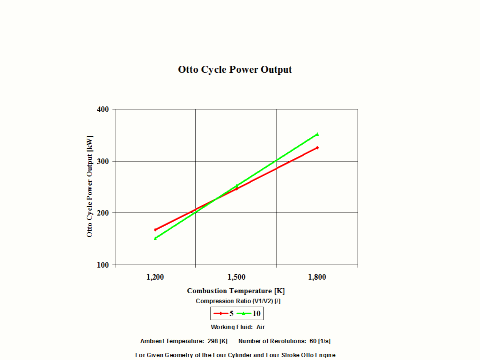
Figure 4 - Otto Cycle Power Output
One can notice that the Otto Cycle efficiency increases with an increase in the compression ratio values. One can notice that the Otto Cycle power output increases with an increase in the combustion temperature. The Otto Cycle power output is greater for the higher compression ratio values.
Assumptions
Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
Governing Equations
T2/T1 = (V1/V2)^(ϰ-1)
V1/V2 = (T2/T1)^1/(ϰ-1)
T3/T4 = (V4/V3)^(ϰ-1)
V4/V3 = (T3/T4)^1/(ϰ-1)
ϰ = cp/cv
cp - cv = R
pv = RT
w = qh - ql
qh = cv(T3 - T2)
ql = cv(T4 - T1)
w = cv(T3 - T2) - cv(T4 - T1)
W = (cv(T3 - T2) - cv(T4 - T1))m
efficiency = 1 - 1/compression ratio^(ϰ-1)
compression ratio = V1/V2
Input Data
T1 = 298 [K]
p1 = 1 [atm]
T3 = 1,200, 1,500 and 1,800 [K]
compression ratio = 2.5, 5, 7.5, 10 and 12.5 [/]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
Results
Otto Cycle Efficiency vs Compression Ratio
Compression
Ratio
[/]
2.5
5
7.5
10
12.5
Otto Cycle
Efficiency
[%]
30.7
47.5
55.3
60.2
63.6
Otto Cycle Power Output
Power Output
[kW]
Compression Ratio
[/]
5
15
Combustion
Temperature
[K]
1,200
167.1
151.2
1,500
246.4
251.7
1,800
325.6
352.2
Conclusions
The Otto Cycle efficiency increases with an increase in the compression ratio values. Also, the Otto Cycle power output increases with an increase in the combustion temperature. The Otto Cycle power output is greater for the higher compression ratio values.
References
JANAF Thermochemical Data - Tables, 1970
Diesel Cycle
Introduction
This section provides a Diesel Cycle analysis when the working fluid is air.
Analysis
In the presented Diesel Cycle analysis, only air is considered as the working fluid behaving as a perfect gas -- specific heat has a constant value. Ideal gas state equation is valid -- pv = RT.
Air enters a cylinder at point 1 when compression starts and it ends at point 2. Isentropic compression is considered with no entropy change. Heat addition starts at point 2 and it ends at point 3. At a constant pressure, air gets heated and the working fluid temperature raises. Expansion starts at point 3 and it ends at point 4. Isentropic expansion is considered with no entropy change. Air heat rejection starts at point 4 and it ends at point 1. At a constant volume, air gets cooled and the working fluid temperature decreases. It should be mentioned that air at point 1 enters the compression process again and the cycle is repeated.
Figure 1 contains a Diesel Cycle pressure vs volume diagram.
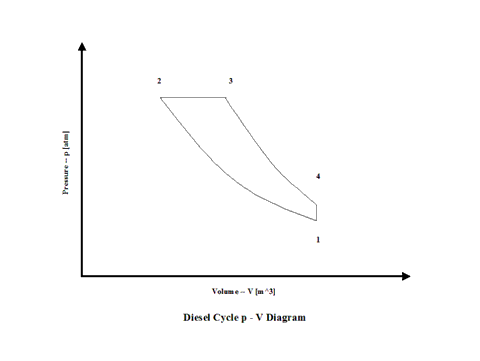
Figure 1 - Diesel Cycle Pressure vs Volume Diagram
Figure 2 presents a Diesel Cycle temperature vs entropy diagram.
igure 1 - Diesel Cycle Pressure vs Volume Diagram
Figure 2 presents a Diesel Cycle temperature vs entropy diagram.
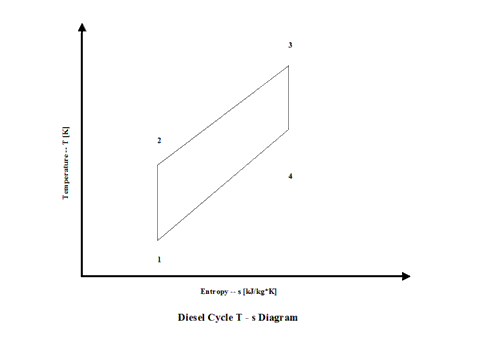
Figure 2 - Diesel Cycle Temperature vs Entropy Diagram
Figure 3 presents the Diesel Cycle efficiency as a function of the compression ratio and a cut off ratio. It should be noted that the inlet conditions are standard ambient conditions: temperature of 298 [K] and absolute pressure of 1 [atm].
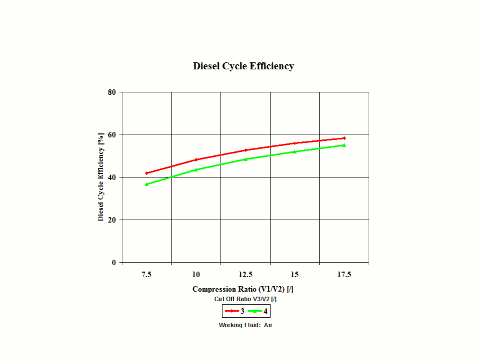
Figure 3 - Diesel Cycle Efficiency
Figure 4 presents the Diesel Cycle power output as a function of compression and combustion temperature values.
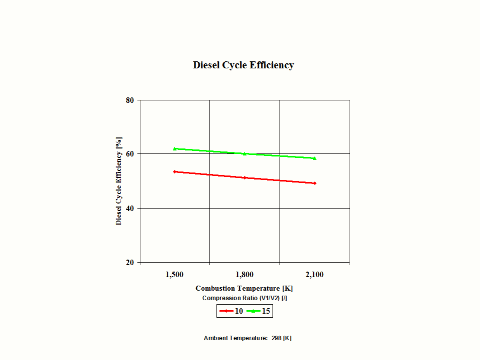
Figure 4 - Diesel Cycle Power Output
Figure 5 presents the Diesel Cycle cut off ratio as a function of the combustion temperature and compression ratio.
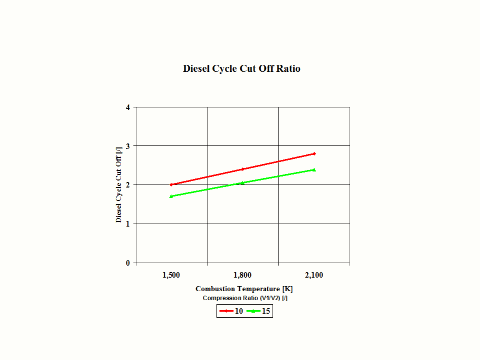
Figure 5 - Diesel Cycle Cut Off Ratio
Figure 6 presents the Diesel Cycle power output as a function of the combustion temperature and compression ratio. It should be noted that the number of revolutions is 60 [1/s] for given geometry of the four cylinder and four stroke Diesel engine.
Figure 5 - Diesel Cycle Cut Off Ratio
Figure 6 presents the Diesel Cycle power output as a function of the combustion temperature and compression ratio. It should be noted that the number of revolutions is 60 [1/s] for given geometry of the four cylinder and four stroke Diesel engine.
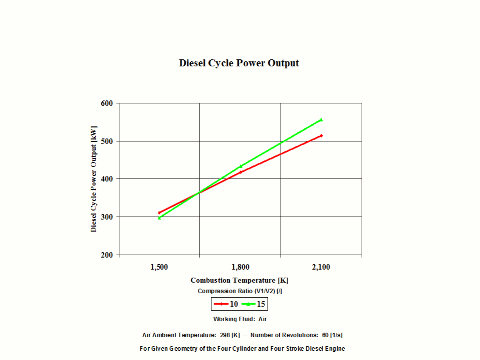
Figure 6 - Diesel Cycle Power Output
One can notice that the Diesel Cycle efficiency increases with an increase in the compression ratio and a decrease of the cut off ratio values. One can notice that the Diesel Cycle power output increases with an increase in the compression ratio and combustion temperature values.
Assumptions
Working fluid is air. There is no friction. Compression and expansion are isentropic -- there is no entropy change. Ideal gas state equation is valid -- pv = RT. Air behaves as a perfect gas -- specific heat has a constant value.
Governing Equations
T2/T1 = (V1/V2)^(ϰ-1)
V1/V2 = (T2/T1)^1/(ϰ-1)
T3/T4 = (V4/V3)^(ϰ-1)
V4/V3 = (T3/T4)^1/(ϰ-1)
ϰ = cp/cv
cp - cv = R
pv = RT
w = qh - ql
qh = cp(T3 - T2)
ql = cv(T4 - T1)
w = cp(T3 - T2) - cv(T4 - T1)
W = (cp(T3 - T2) - cv(T4 - T1))m
efficiency = 1 - (cut off ratio^ϰ - 1)/(ϰ(compression ratio^(ϰ-1))(cut off ratio - 1))
compression ratio = V1/V2
cut off ratio = V3/V2
Input Data
T1 = 298 [K]
p1 = 1 [atm]
compression ratio = 7.5, 10, 12.5, 15 and 17.5 [/]
cut off ratio = 3 and 4 [/]
R = 0.2867 [kJ/kg*K]
cp = 1.004 [kJ/kg*K]
ϰ = 1.4 [/]
Results
Diesel Cycle Efficiency
Diesel Cycle Efficiency
[%]
Cut Off Ratio
[/]
3
4
7.5
41.69
36.57
Compression
Ratio
[/]
10
48.03
43.4
12.5
52.46
48.29
15
55.81
51.93
17.5
58.45
54.80
Diesel Cycle Efficiency
Diesel Cycle
Efficiency
[%]
Compression Ratio
[/]
10
15
Combustion
Temperature
[K]
1,500
53.39
61.94
1,800
51.12
60.12
2,100
49.20
58.49
Diesel Cycle Cut Off Ratio
Cut Off Ratio
[/]
Compression Ratio
[/]
10
15
Combustion
Temperature
[K]
1,500
2.00
1.70
1,800
2.40
2.05
2,100
2.80
2.39
Diesel Cycle Power Output
Power Output
[kW]
Compression Ratio
[/]
10
15
Combustion
Temperature
[K]
1,500
311
297
1,800
417
433
2,100
514
557
Conclusions
The Diesel Cycle efficiency increases with an increase in the compression ratio and a decrase in the cut off rati values. Also, the Diesel Cycle power output increases with an increase in the compression ratio and combustion temperature values.
References
JANAF Thermochemical Data - Tables, 1970